Metodi numerici di integrazione¶
Al termine del capitolo precedente siamo incappati in un integrale impossibile da risolvere con le tecniche di calcolo alla nostra portata e per questo ci siamo avvalsi del risultato fornito da un programma adatto. Possiamo evitare l’uso di un software specifico. Con un linguaggio di programmazione possiamo implementare algoritmi che simulano l’attività di questi software. Otterremo risultati approssimati, interessanti per i metodi che utilizzati, più che per i valori in sè. Come già si è visto per il calcolo differenziale, questi metodi si dicono metodi numerici.
Il metodo dei rettangoli¶
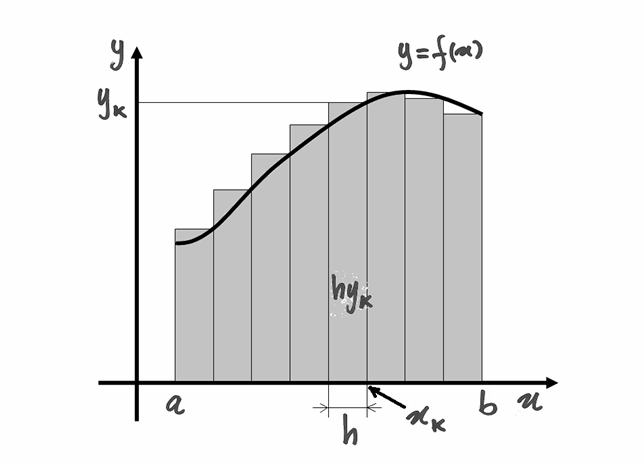
Il primo metodo che studiamo è il più semplice, ma anche il meno preciso. L’intervallo di integrazione viene suddiviso in un numero finito di parti, che quindi sono piccole ma non infinitesime.
Data la funzione continua ![f:[a,b] \to \mathbf{R}](../../../_images/math/f3e75393e9ff61c6649d44c1124a41bdd0d27876.png) , costruiamo una successione
di
, costruiamo una successione
di 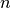 punti in modo che sia
punti in modo che sia 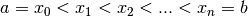 . In ogni
sottointervallo
. In ogni
sottointervallo ![[x_k,x_{k+1}]](../../../_images/math/5446057f54ec360dabac9be7e526d7787a2a6a0f.png) prendiamo un numero
prendiamo un numero 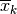 e approssimiamo l’integrale
e approssimiamo l’integrale 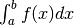 con la somma
con la somma
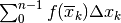 .
.
Si potrebbe, per semplificare,
distanziare ugualmente i punti. Allora, per ogni 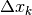 abbiamo
abbiamo
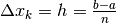 e
e 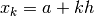 , con
, con 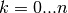 . Se
prendiamo come altezza di ogni rettangolo il valore della funzione nell’estremo
destro della base,
. Se
prendiamo come altezza di ogni rettangolo il valore della funzione nell’estremo
destro della base, 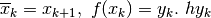 è l’area
di ogni rettangolo e la somma che approssima l’integrale diventa:
è l’area
di ogni rettangolo e la somma che approssima l’integrale diventa:
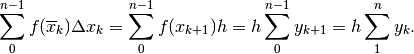
Ne risulta quindi l’uguaglianza approssimata:
Questa è la formula alla quale facciamo riferimento per costruire l’algoritmo che svolgerà i primi calcoli.
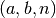
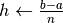 ;
;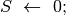
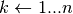 esegui
esegui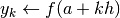 ;
;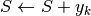 ;
;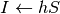
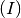
Due esempi¶
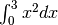 .
.
Calcoliamo con questo metodo un integrale facile: 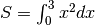 , il cui
valore esatto è
, il cui
valore esatto è 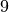 .
.
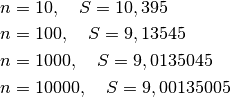
Man mano che cresce il numero degli intervalli, e l’algoritmo prevede un maggior numero di cicli, il risultato approssima sempre meglio quello esatto.
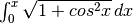 .
.
L’integrale impossibile del capitolo
precedente, cioè 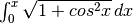 viene calcolato con la
stessa precisione prevedendo
viene calcolato con la
stessa precisione prevedendo 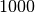 cicli.
cicli.
Il metodo dei trapezi¶
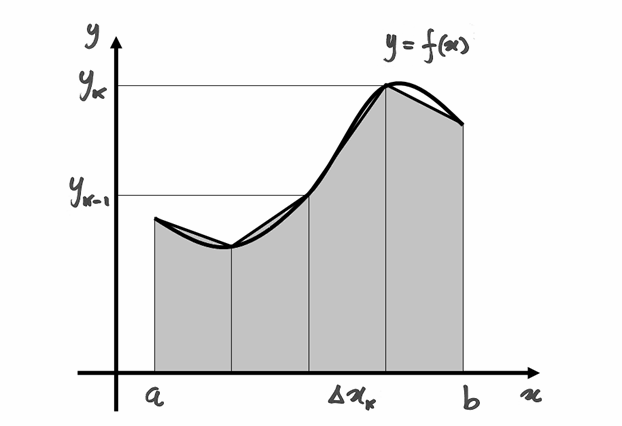
Come indica il nome, questo metodo si basa sulla sostituzione dei rettangoli
con i trapezi. Il grafico della funzione viene approssimato da una spezzata,
che è il grafico di una funzione approssimante 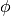 , una funzione
lineare a tratti. In pratica il valore di
, una funzione
lineare a tratti. In pratica il valore di 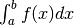 si approssima con il valore esatto di
si approssima con il valore esatto di 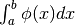 .
.
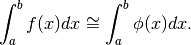
Manteniamo la stessa suddivisione in intervalli adottata con il metodo dei rettangoli.
Data 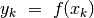 , definiamo la funzione
, definiamo la funzione 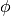 come la funzione che ha
per grafico la spezzata che unisce i punti
come la funzione che ha
per grafico la spezzata che unisce i punti 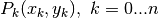 .
.
L’area di ogni trapezio è data da 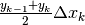 , quindi
, quindi
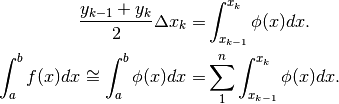
Possiamo quindi scrivere la formula approssimata
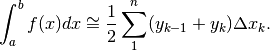
Nella suddivisione in progressione aritmetica, ogni sottointervallo ha ampiezza
costante: 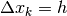 e quindi si ha:
e quindi si ha:
![\int_a^bf(x)dx\cong &\frac{h}{2}\sum_1^n (y_{k-1}+y_k)=\\
=&\frac{h}{2}[(y_0+y_1)+(y_1+y_2)+(y_2+y_3)+ ... +(y_{n-1}+y_n)]=\\
=&\frac{h}{2}(y_0+2y_1+2y_2+2y_3+ ... +2y_{n-1}+y_n)=\\
=&\frac{h}{2}\left[y_0+2\sum_1^{n-1}y_k+y_n \right].](../../../_images/math/92677eec42cee71c2b66d7edf216f589fb8d566a.png)
L’algoritmo allora è:
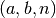 ;
;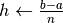 ;
;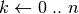 esegui
esegui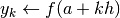 ;
;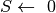 ;
;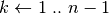 esegui
esegui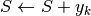 ;
;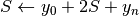 ;
;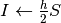 ;
;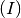 ;
;Se si testa il funzionamento dell’algoritmo sulla funzione 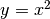 si scopre che per
si scopre che per 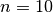 , cioè ricoprendo la superficie con
, cioè ricoprendo la superficie con 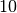 trapezi, si ottiene quasi la stessa precisione ottenuta con
trapezi, si ottiene quasi la stessa precisione ottenuta con 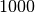 rettangoli.
rettangoli.
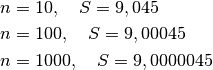
Il segno dell’area¶
Osservando il disegno della pagina precedente, si può notare come il ricoprimento a trapezi sia più efficace di quello fatto a rettangoli.
C’è un dettaglio da discutere nel caso che il tratto obliquo intersechi l’asse
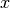 : il segno dell’area risulta positivo o negativo?
: il segno dell’area risulta positivo o negativo?
Supponiamo di avere 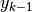 negativo e in valore assoluto minore rispetto
a
negativo e in valore assoluto minore rispetto
a 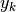 positivo:
positivo: 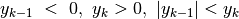 . Al
numeratore della formula dell’area del trapezio c’è la somma
. Al
numeratore della formula dell’area del trapezio c’è la somma 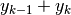 ,
che vale in questo caso
,
che vale in questo caso 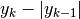 (ma gli altri casi sono analoghi).
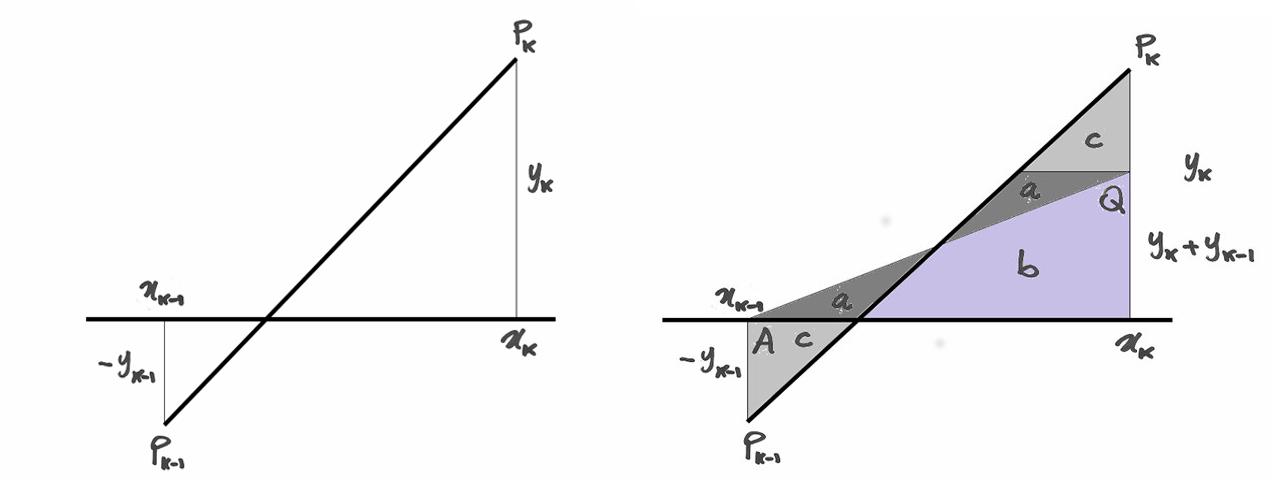
Fissiamo il punto
(ma gli altri casi sono analoghi).
Fissiamo il punto 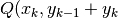 ), quindi di ordinata corrispondente
alla somma delle basi del trapezio. Uniamo
), quindi di ordinata corrispondente
alla somma delle basi del trapezio. Uniamo 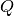 con
con 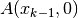 .
Si formano così 4 triangoli
.
Si formano così 4 triangoli 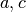 uguali a coppie, e un quadrilatero
uguali a coppie, e un quadrilatero 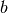 .
Nel calcolare l’area del trapezio, i triangoli
.
Nel calcolare l’area del trapezio, i triangoli  si annullano e la parte
restante
si annullano e la parte
restante 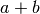 , sottesa al segmento, equivale al triangolo
, sottesa al segmento, equivale al triangolo 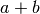 ,
con ipotenusa
,
con ipotenusa 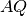 . Se
. Se 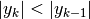 lo stesso disegno si ripropone
nel semipiano negativo, e anche i casi in cui
lo stesso disegno si ripropone
nel semipiano negativo, e anche i casi in cui 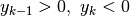 sono
analoghi.
In conclusione, la formula
sono
analoghi.
In conclusione, la formula 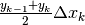 produce
l’area effettiva del trapezio, tenendo conto correttamente di tutte le parti,
negative e positive.
produce
l’area effettiva del trapezio, tenendo conto correttamente di tutte le parti,
negative e positive.
La formula di Simpson¶
Con il ricoprimento a trapezi la funzione è stata trasformata in una funzione a dominio discreto e per ogni coppia di suoi punti al posto della funzione originale abbiamo usato una funzione lineare. Si è trattato quindi di una interpolazione lineare.
Procediamo ora sulla stessa falsariga, isolando non coppie ma terne di punti
consecutivi e considerando, al posto della funzione, l’arco di parabola per quei
punti. Il grafico che passa per tre punti è infatti espressione di un polinomio
al massimo di secondo grado (al massimo di primo grado se i tre punti sono
allineati, di grado zero se sono allineati in orizzontale).
Se dobbiamo considerare gruppi di tre punti, gli intervallini
saranno necessariamente in numero pari, quindi 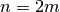 . Limitiamoci anche
questa volta a intervallini di uguale ampiezza
. Limitiamoci anche
questa volta a intervallini di uguale ampiezza 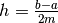 .
.
Procediamo con i primi tre punti 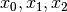 e poi cercheremo di
generalizzare il risultato. Il fatto importante, però, non è tanto esprimere il
polinomio, quanto il suo integrale in
e poi cercheremo di
generalizzare il risultato. Il fatto importante, però, non è tanto esprimere il
polinomio, quanto il suo integrale in ![[x_0,x_2]](../../../_images/math/bafaaeba23d51aea45af830ef7b33ea4cff06b70.png) . Stiamo infatti cercando
di sostituire la funzione
. Stiamo infatti cercando
di sostituire la funzione 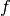 con una funzione
con una funzione 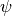 che coincide
con l’unico polinomio passante per i tre punti consecutivi, che isolano una coppia
di intervallini. E deve valere che l’integrale approssimato di
che coincide
con l’unico polinomio passante per i tre punti consecutivi, che isolano una coppia
di intervallini. E deve valere che l’integrale approssimato di 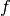 è
l’integrale esatto di
è
l’integrale esatto di 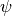 , il quale a sua volta è la somma di una coppia
di integrali:
, il quale a sua volta è la somma di una coppia
di integrali:
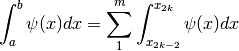
Il primo di questi integrali è
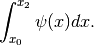
La funzione 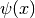 , come abbiamo detto è un polinomio al massimo di
secondo grado:
, come abbiamo detto è un polinomio al massimo di
secondo grado: 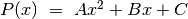 , del quale sappiamo che
, del quale sappiamo che
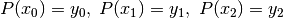 , con
, con 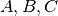 da ricavare.
da ricavare.
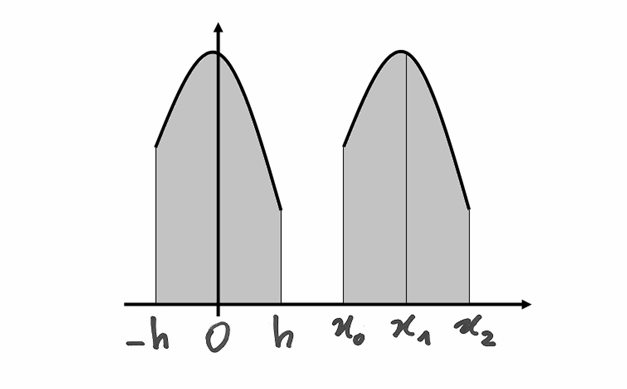
Per facilitare la ricerca di questi tre coefficienti (e poiché, in fondo, ci
interessa più l’integrale del polinomio), ricordiamoci che gli intervallini
hanno uguale ampiezza 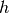 : potremo allora traslare i due intervallini:
: potremo allora traslare i due intervallini:
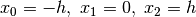 , mantenendo, ovviamente, uguali valori per
gli
, mantenendo, ovviamente, uguali valori per
gli 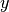 corrispondenti.
Il vantaggio di questa trasformazione è che ora dobbiamo calcolare
corrispondenti.
Il vantaggio di questa trasformazione è che ora dobbiamo calcolare
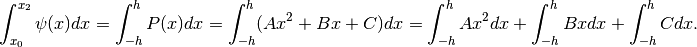
Poiché ora abbiamo l’intervallo di integrazione simmetrico, le funzioni dispari hanno integrale nullo mentre le funzioni pari hanno integrale doppio rispetto all’integrale su metà intervallo:
![\int_{-h}^{h}(Ax^2+Bx+C)dx= 2 \int_0^{h}(Ax^2+C)dx
=2\left[\frac{Ah^3}{3}+Cx\right]_0^h=\frac{2}{3}Ah^3+2Ch.](../../../_images/math/29b1714d56b3184d598559384bb85bde9f5b7215.png)
Abbiamo così scoperto che il calcolo di 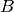 non è importante. Poi, da
non è importante. Poi, da
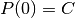 segue
segue 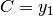 . Per il calcolo di
. Per il calcolo di 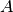 :
:
![&P(-h)=Ah^2-Bh+C=y_0\\
&P(h)=Ah^2+Bh+C=y_2\\
&P(-h)+P(h)=2Ah^2+2C=y_0+y_2\\
&2Ah^2=y_0-2y_1+y_2\\
&\int_{-h}^{h}(Ax^2+Bx+C)dx=\frac{2}{3}Ah^3+2Ch=\frac{h}{3}\left[2Ah^2+6C \right]=
\frac{h}{3}(y_0+4y_1+y_2).](../../../_images/math/80ad3d712c4a4460d8861c11582ba1ced69a2072.png)
Abbiamo quindi trovato l’integrale dell’arco di parabola per i primi tre punti, in
funzione dell’ampiezza 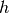 degli intervallini e delle ordinate dei tre punti.
La cosa si estende facilmente a tutte le terne di punti successive, così:
degli intervallini e delle ordinate dei tre punti.
La cosa si estende facilmente a tutte le terne di punti successive, così:
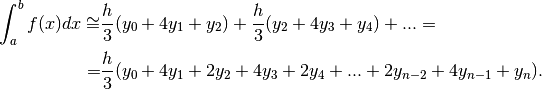
Tranne che per il primo e per l’ultimo termine, sui termini di indice pari si
raddoppia la somma, mentre sui termini di indice dispari si quadruplica.
Ricordando che 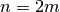 , riscriviamo e sintetizziamo:
, riscriviamo e sintetizziamo:
![\int_a^bf(x)dx\cong &\frac{h}{3}(y_0+4y_1+2y_2+ ... +2y_{2m-2}+4y_{2m-1}+y_{2m})=\\
&=\frac{h}{3}\left[y_0+4\sum_1^m y_{2k-1}+2\sum_1^{m-1}y_{2k}+y_{2m} \right].](../../../_images/math/80b9a9c252eaadfdfdd0abc8c52a1007995fe168.png)
Questa formula è detta di Simpson, o di integrazione parabolica. L’algoritmo allora è
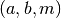 ;
;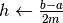 ;
;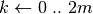 esegui
esegui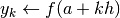 ;
;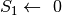 ;
;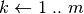 esegui
esegui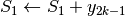 ;
;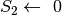 ;
;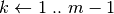 esegui
esegui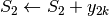 ;
;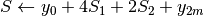 ;
;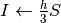 ;
;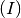 ;
;La precisione della formula di Simpson¶
Calcolare con questo algoritmo l’integrale di una funzione di secondo grado non ha molto senso, perché l’interpolazione della parabola, fatta con una parabola, non può che dare il risultato esatto.
È meno ovvio che risulti esatto anche l’integrale di una cubica. Infatti, se si
impiega l’algoritmo per calcolare 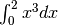 anche solo con due
intervalli, cioè
anche solo con due
intervalli, cioè 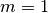 , si ottiene il risultato esatto, cioè
, si ottiene il risultato esatto, cioè 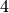 .
.
Vediamolo in dettaglio. Con 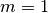 ci sono due intervalli e i punti
sono
ci sono due intervalli e i punti
sono 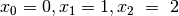 . I valori corrispondenti di
. I valori corrispondenti di 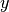 sono:
sono:
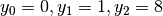 . Poiché
. Poiché 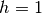 , la formula di Simpson dà:
, la formula di Simpson dà:
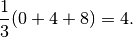
Il polinomio interpolatore 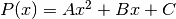 , al massimo di secondo grado, è
caratterizzato da
, al massimo di secondo grado, è
caratterizzato da 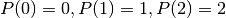 . Date queste condizioni, abbiamo
. Date queste condizioni, abbiamo
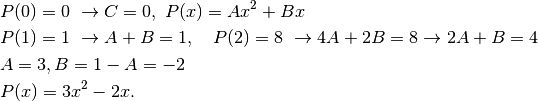
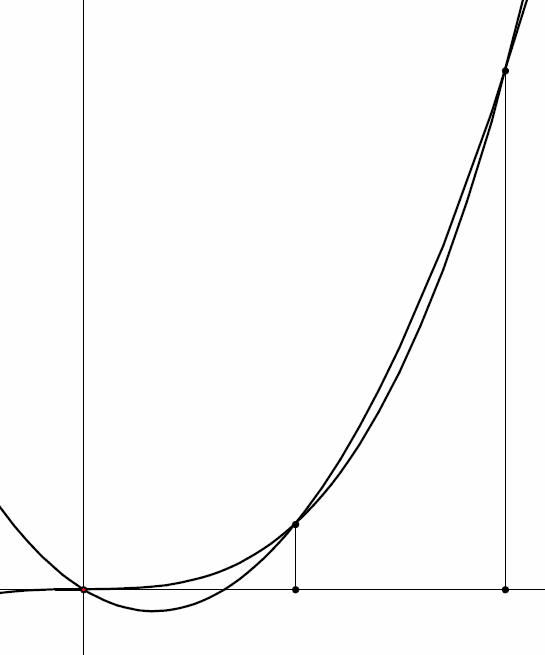
I grafici della funzione e del polinomio sono ovviamente diversi, ma gli integrali coincidono:
![\int_0^2(3x^2-2x)dx=[x^3-x^2]_0^2=8-4=4.](../../../_images/math/79b63d121202700a91a5c75cc483bb65058c4a01.png)
La cosa notevole è che la formula di Simpson fornisce il risultato esatto per tutti
i polinomi di terzo grado. Infatti in questi polinomi l’unica parte da discutere
è il termine in 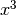 , perchè i termini di grado inferiore coincidono con
la loro interpolazione, come abbiamo già notato. Discutiamo quindi solo di
, perchè i termini di grado inferiore coincidono con
la loro interpolazione, come abbiamo già notato. Discutiamo quindi solo di
![\int_a^b x^3dx=\left[\frac{x^4}{4} \right]_a^b=\frac{b^4-a^4}{4}.](../../../_images/math/a07c1626793127dcca7bb5419261ed647b4f6e68.png)
Con la formula di Simpson, con 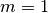 , abbiamo:
, abbiamo:
![& x_0=a,\quad x_1=\frac{a+b}{2},\quad x_2=b.\\
&y_0=a^3,\quad y_1=\frac{(a+b)^3}{8},\quad y_2=b^3.\\
&h=\frac{a+b}{2}.\\
&\frac{h}{3}(y_0+4y_1+y_2)=\frac{b-a}{6}\left[ a^3+\frac{(a+b)^3}{2}+b^3\right]=
\frac{b^4-a^4}{4}](../../../_images/math/a28429eb11c0ff4ad422be88dc14b74da15bdbff.png)
come si verifica facilmente sviluppando la parentesi quadrata. Il risultato è anche indipendente dal numero di intervalli, perché se vale per una coppia di intervalli, vale anche per ogni altro numero di coppie. La ragione di questa esattezza risiede nel fatto, dimostrabile, che l’imprecisione della formula di Simpson dipende dai valori della derivata quarta della funzione, che vale zero nel nostro polinomio.
I tre metodi a confronto¶
Vale la pena di testare i tre metodi descritti, per calcolare un integrale di cui non
conosciamo la primitiva: 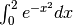 .
.
Ecco la tabella che registra i risultati di prove diverse.
| intervalli | rettangoli | trapezi | Simpson |
|---|---|---|---|
| 10 | 0,71460477 | 0,7462108 | 0,74682495 |
| 20 | ... | ... | 0,74682418 |
| 40 | ... | ... | 0,74682414 |
| 1000 | 0,74650801 | 0,74682407 | ... |
| 10000 | ... | 0,74682413 | ... |
| 1000000 | 0,74682382 | ... | ... |
Il risultato che si ottiene con Derive, un software dedicato, è 0,74682413.
Derive usa un numero di suddivisioni dell’ordine del miliardo e per questo
posiamo prendere il suo risultato come il più preciso. Si può notare
che il metodo di Simpson raggiunge l’esattezza fino alla settima cifra decimale
con 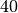 intervalli (
intervalli (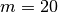 ), una precisione uguagliata dal metodo
dei trapezi con
), una precisione uguagliata dal metodo
dei trapezi con 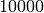 intervalli.
intervalli.
Il metodo Montecarlo¶
Il metodo Montecarlo ha un’origine e un’impostazione del tutto diverse dai precedenti. Proviene infatti da studi di statistica e il suo nome ricorda il gioco d’azzardo e i numeri che escono a caso. Applichiamo i concetti di questo metodo al calcolo degli integrali.
Abbiamo una funzione 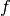 continua e positiva su
continua e positiva su ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) e conosciamo
anche un maggiorante della funzione, cioè un numero
e conosciamo
anche un maggiorante della funzione, cioè un numero 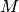 tale che
tale che
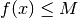 per ogni
per ogni ![x\in [a,b]](../../../_images/math/cb9ed72f8db4b1233bb65701d2fc295ba6138b74.png) . Il trapezoide della funzione
è certamente contenuto nel rettangolo di base l’intervallo
. Il trapezoide della funzione
è certamente contenuto nel rettangolo di base l’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) e
altezza
e
altezza 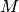 .
.
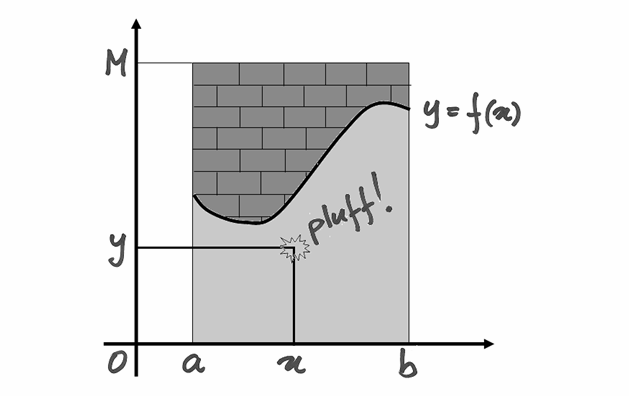
Per capirci, possiamo immaginare che il trapezoide sia la vasca di una piscina e
la parte restante del rettangolo sia il bordo piastrellato della vasca. Gettando
casualmente sassi sul rettangolo, la probabilità che cadano nell’acqua è legata
all’area del trapezoide. Per esempio, se 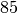 % dei sassi cade in acqua,
diremo che l’area della vasca è
% dei sassi cade in acqua,
diremo che l’area della vasca è 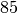 % dell’area del rettangolo. Quindi,
se cade in acqua la frazione
% dell’area del rettangolo. Quindi,
se cade in acqua la frazione 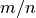 dei lanci, questa è la nostra stima
dell’area del trapezoide:
dei lanci, questa è la nostra stima
dell’area del trapezoide:
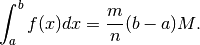
Ovviamente, dovremo avere lanciato in modo omogeneo, senza concentrare i lanci su
un’area piuttosto che su un’altra. I lanci devono essere quindi casuali e
distribuiti in modo omogeneo su tutto il rettangolo. Quindi le coordinate del punto
in cui arriva ogni lancio devono essere calcolate da una funzione opportuna,
che fornisce numeri uniformemente distribuiti e indipendenti, come si richiede a
numeri correttamente casuali. Uniformemente distribuiti significa che in ogni
porzione dell’intervallo cade più o meno la stessa quantità di numeri.
Indipendenti significa che ogni numero non è legato al numero generato in precedenza.
Se queste caratteristiche sono rispettate, allora il caso viene simulato
abbastanza bene. Esiste un algoritmo apposito, implementato nei software, detto
generatore di numeri pseudocasuali, che garantisce un buon rispetto di queste
regole. I numeri di questo generatore sono compresi fra  e
e 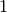 e
si ripetono all’incirca dopo milioni di volte, in modo che, generato un numero,
è impossibile prevedere il successivo. La funzione dei sofware che implementa
la generazione di questi numeri è detta random e noi la richiameremo con il
comando rnd.
e
si ripetono all’incirca dopo milioni di volte, in modo che, generato un numero,
è impossibile prevedere il successivo. La funzione dei sofware che implementa
la generazione di questi numeri è detta random e noi la richiameremo con il
comando rnd.
Dunque, dobbiamo generare casualmente punti nel rettangolo ![[a,b]\times[0,m]](../../../_images/math/f7db5315b05c77a12146f1e96af9279c217d17e2.png) ,
con il generatore di numeri pseudocasuali rnd, che fornisce numeri fra
,
con il generatore di numeri pseudocasuali rnd, che fornisce numeri fra  e
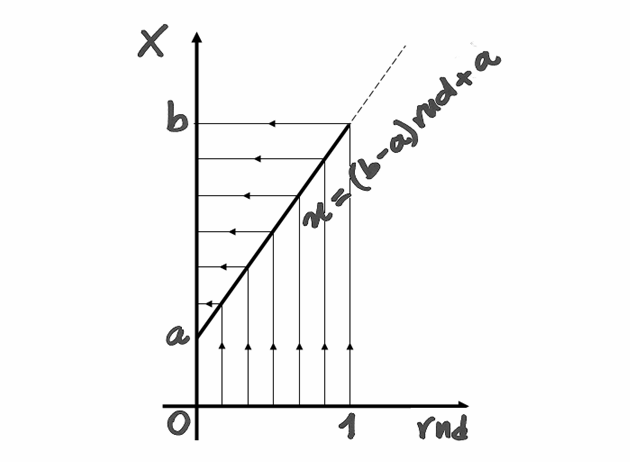
e 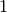 . Avremo quindi coppie di numeri da trasformare, in modo che risultino
appartenere all’intervallo voluto. La funzione che trasforma questi numeri è una
semplice retta. Infatti, perché un numero casuale
. Avremo quindi coppie di numeri da trasformare, in modo che risultino
appartenere all’intervallo voluto. La funzione che trasforma questi numeri è una
semplice retta. Infatti, perché un numero casuale ![\mathit{rnd} \in [0,1]](../../../_images/math/9d52db6b2f79ab7082d3546e3c7ccd653bab614b.png) sia trasformato in un numero dell’intervallo
sia trasformato in un numero dell’intervallo ![x\in[a,b]](../../../_images/math/7c8b59f5de2942ccf6e4c7bd246b1d1bbdc1e383.png) , basta che sia
, basta che sia
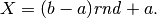
Analogamente, dovrà essere 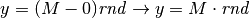 .
.
Per costruire l’algoritmo che conta quanti punti casuali appartengono all’area
richiesta abbiamo bisogno di controllare se la coordinata 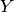 dei punti
è nel trapezoide, cioè se ha valore inferiore a quello corrispondente della
funzione:
dei punti
è nel trapezoide, cioè se ha valore inferiore a quello corrispondente della
funzione: 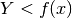 .
.
L’algoritmo riceve in ingresso il numero 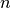 di lanci, cioè di valori casuali
da generare, e gli intervalli entro cui trasformarli. Poi incrementa un
contatore
di lanci, cioè di valori casuali
da generare, e gli intervalli entro cui trasformarli. Poi incrementa un
contatore 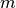 ogni volta che il numero
ogni volta che il numero 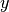 è inferiore a
è inferiore a 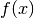 e infine produce la frazione
e infine produce la frazione 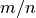 che, moltiplicata per l’area del rettangolo,
fornisce la stima dell’integrale.
che, moltiplicata per l’area del rettangolo,
fornisce la stima dell’integrale.
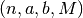 ;
;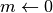
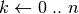 esegui
esegui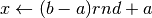 ;
;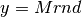 ;
;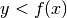 allora
allora 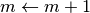 ;
;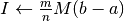 ;
;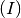 ;
;Un test per il metodo Montecarlo¶
Proviamo il metodo sul calcolo di 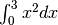 e confrontiamolo con i
risultati dei metodi precedenti e con il risultato esatto che conosciamo, cioè
e confrontiamolo con i
risultati dei metodi precedenti e con il risultato esatto che conosciamo, cioè 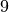 .
Come maggiorante useremo
.
Come maggiorante useremo 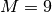 .
.
| lanci | Montecarlo |
|---|---|
| 10 | 8,1 |
| 100 | 10,8 |
| 1000 | 8,937 |
| 10000 | 9,0315 |
| 100000 | 8,99532 |
| 1000000 | 8,967537 |
Osserviamo che il metodo è impreciso e non è detto che aumentare il numero
dei lanci migliori la precisione. Si tratta di un metodo statistico, cioè
che produce risultati in media vicini al valore esatto. Infatti lo stesso
gruppo di lanci non dà, in genere, lo stesso risultato. Bisogna quindi
ripetere i gruppi di lanci e fare la media. Per esempio si trova che ripetendo
dieci volte 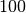 lanci, il risultato medio è
lanci, il risultato medio è 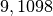 .
In conclusione, il metodo Montecarlo non è da usare per un integrale definito,
cosa che d’altronde ci era nota anche in relazione agli altri metodi.
In effetti il metodo Montecarlo eccelle in altre situazioni.
.
In conclusione, il metodo Montecarlo non è da usare per un integrale definito,
cosa che d’altronde ci era nota anche in relazione agli altri metodi.
In effetti il metodo Montecarlo eccelle in altre situazioni.
Possiamo provare ad applicarlo all’integrale 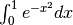 Con
Con 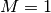 e
e  lanci un risultato è
lanci un risultato è 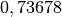 , che
è un’ottima approssimazione del risultato a
, che
è un’ottima approssimazione del risultato a 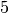 decimali ottenuto
con Derive.
decimali ottenuto
con Derive.
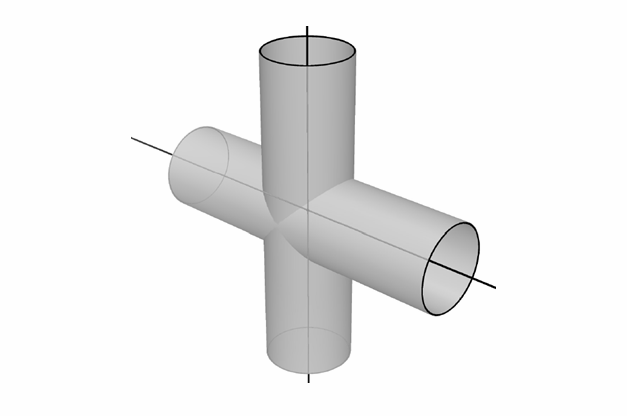
Un problema di stima¶
Due cilindri si intersecano perpendicolarmente. Occorre una stima del volume comune ai due cilindri.
Il volume cercato è proporzionale a 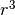 , con
, con  raggio dei
cilindri. Per semplificare poniamo
raggio dei
cilindri. Per semplificare poniamo 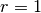 . Immaginiamo che gli assi dei
due cilindri coincidano con gli assi cartesiani
. Immaginiamo che gli assi dei
due cilindri coincidano con gli assi cartesiani 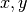 . Lungo l’asse
. Lungo l’asse 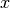 si sviluppa il volume interno al cilindro orizzontale, caratterizzato dalla
disequazione
si sviluppa il volume interno al cilindro orizzontale, caratterizzato dalla
disequazione 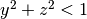 . Per il cilindro verticale c’è una disequazione
analoga:
. Per il cilindro verticale c’è una disequazione
analoga: 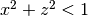 . La regione comune ai due cilindri è contenuta in un
volume cubico di lato
. La regione comune ai due cilindri è contenuta in un
volume cubico di lato 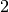 e quindi volume
e quindi volume 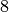 .
.
Ora fingiamo che il volume cubico sia un panettone e di volerci conficcare dei
canditi a caso. Dopo avere inserito 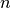 canditi in posizione casuale,
rileveremo quanti di essi sono nel volume comune ai due cilindri. La frazione
canditi in posizione casuale,
rileveremo quanti di essi sono nel volume comune ai due cilindri. La frazione
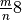 sarà la stima richiesta.
sarà la stima richiesta.
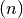 ;
;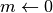
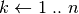 esegui
esegui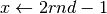 ;
;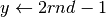 ;
; ;
;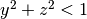 AND
AND 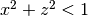 allora
allora 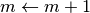 ;
;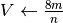 ;
;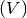 ;
;Il controllo sulla posizione di ogni candito avviene attraverso la verifica delle
due disequazioni. L’intervallo entro cui far cadere i numeri pseudocasuali è
![[-1,1]](../../../_images/math/11d586f6b5c3a0445fa328423430a9390fd2834b.png) e quindi ogni numero si ottiene da
e quindi ogni numero si ottiene da
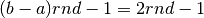 .
.
L’algoritmo genera un risultato che si assesta attorno a 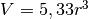 ,
con un milione di canditi. Il metodo Montecarlo ci consente di stimare rapidamente
un integrale non facile, senza impegnarci in calcoli: è questo il suo vantaggio
principale.
,
con un milione di canditi. Il metodo Montecarlo ci consente di stimare rapidamente
un integrale non facile, senza impegnarci in calcoli: è questo il suo vantaggio
principale.
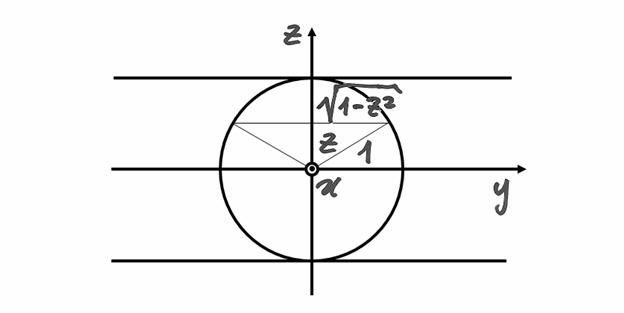
La soluzione esatta¶
Il problema precedente ha una soluzione esatta, che proviamo a calcolare.
Visto da  , l’incrocio dei due cilindri avviene lungo segmenti
inclinati di
, l’incrocio dei due cilindri avviene lungo segmenti
inclinati di 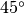 rispetto agli assi dei cilindri (in realtà,
dall’esterno non si vedono segmenti, ma curve).
rispetto agli assi dei cilindri (in realtà,
dall’esterno non si vedono segmenti, ma curve).
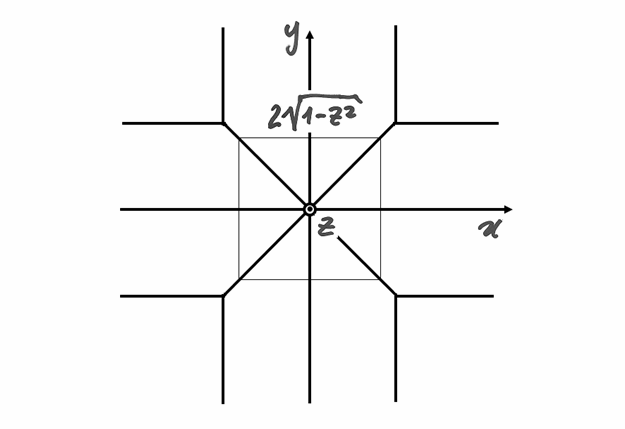
La parte comune ai due cilindri può essere sezionata con piani perpendicolari
all’asse  , formando scaglie quadrate. A distanza
, formando scaglie quadrate. A distanza  dall’origine,
una scaglia ha il lato che misura
dall’origine,
una scaglia ha il lato che misura 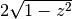 e ha quindi l’area di
e ha quindi l’area di
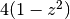 . Ogni scaglia ha spessore infinitesimo
. Ogni scaglia ha spessore infinitesimo 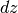 ed è
indistinguibile da un prisma a base quadrata, per cui l’integrale esatto si
calcola così:
ed è
indistinguibile da un prisma a base quadrata, per cui l’integrale esatto si
calcola così:
![4\int_{-1}^1(1-z^2)dz=8\int_0^1(1-z^2)dz=8\left[z-\frac{z^3}{3} \right]_0^1
=\frac{16}{3}.](../../../_images/math/c263d4a49dc587b952cccd9e6a5cde4606c3ada1.png)
Il risultato corrisponde pienamente a quanto calcolato con il metodo Montecarlo e ne conferma la potenza.
La densità dei numeri casuali¶
Negli esempi precedenti ci siamo avvalsi del generatore di numeri pseudocasuali
rnd, implementato nei linguaggi di programmazione, e abbiamo visto che è
sufficientemente affidabile per i nostri scopi. Abbiamo visto anche che i numeri
rnd, generati nell’intervallo ![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) , possono essere trasformati in
altri numeri
, possono essere trasformati in
altri numeri 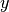 nell’intervallo desiderato
nell’intervallo desiderato ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , grazie alla
funzione di trasferimento
, grazie alla
funzione di trasferimento 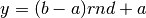 , il cui grafico è una retta.
L’intervallo
, il cui grafico è una retta.
L’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) viene allora riempito di numeri casuali in modo
omogeneo, cioè senza che si addensino preferibilmente in una zona dell’intervallo.
viene allora riempito di numeri casuali in modo
omogeneo, cioè senza che si addensino preferibilmente in una zona dell’intervallo.
Tuttavia proprio questa condizione di uniformità, in genere desiderata, potrebbe
in qualche caso non essere preferibile. Si vorrebbe quindi poter guidare la
distribuzione di questi numeri nell’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , in modo che alcune
zone dell’intervallo siano preferite rispetto ad altre e quindi vi sia una
distribuzione disomogenea, più concentrata in alcune zone rispetto ad altre.
, in modo che alcune
zone dell’intervallo siano preferite rispetto ad altre e quindi vi sia una
distribuzione disomogenea, più concentrata in alcune zone rispetto ad altre.
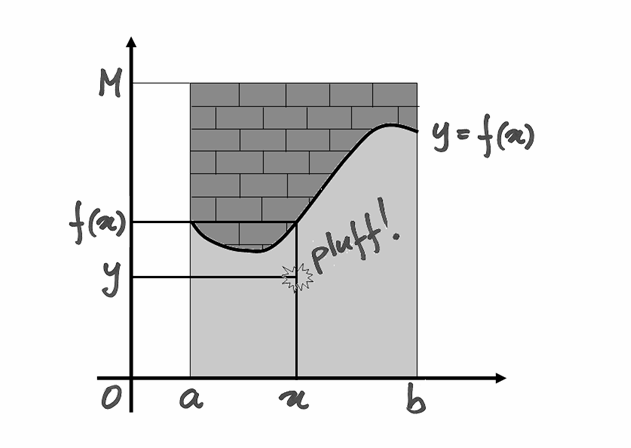
Per esempio, con una funzione come quella in grafico nel disegno, i numeri rnd
vengono generati uniformemente nell’intervallo ![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) , ma si concentrano
agli estremi dell’intervallo di arrivo.
La loro concentrazione è guidata dall’andamento della curva, e quindi dalla
derivata della funzione in grafico.
, ma si concentrano
agli estremi dell’intervallo di arrivo.
La loro concentrazione è guidata dall’andamento della curva, e quindi dalla
derivata della funzione in grafico.
In generale, ogni punto 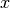 dell’intervallo di arrivo
dell’intervallo di arrivo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) è
legato alla probabilità che siano generati numeri
è
legato alla probabilità che siano generati numeri 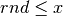 . Per esempio
la probabilità legata a
. Per esempio
la probabilità legata a 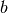 è la certezza, cioè
è la certezza, cioè 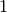 , mentre la
probabilità legata a
, mentre la
probabilità legata a  è così piccola da poter essere considerata nulla.
Chiamiamo
è così piccola da poter essere considerata nulla.
Chiamiamo 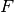 la funzione che rappresenta questa probabilità. Si tratta
di una funzione non decrescente.
la funzione che rappresenta questa probabilità. Si tratta
di una funzione non decrescente. 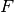 ha caratteristiche analoghe
alla massa di una barra, nulla all’inizio e pari a quella di tutta la barra,
all’estremo opposto. Lavoreremo su funzioni di probabilità crescenti e continue,
per comodità di ragionamento.
ha caratteristiche analoghe
alla massa di una barra, nulla all’inizio e pari a quella di tutta la barra,
all’estremo opposto. Lavoreremo su funzioni di probabilità crescenti e continue,
per comodità di ragionamento.
Nel caso della barra avevamo definita una densità (di massa).
Densità media, che è costante per la barra omogenea, e densità puntuale, quando
la concentrazione della massa varia da punto a punto.
Lo stesso possiamo dire della densità di probabilità. La densità di probabilità
media in un tratto è il rapporto fra la probabilità che in quel tratto cadano i
valori (generati casualmente e trasformati) e la lunghezza del tratto. Per un
tratto ![[x,x+\Delta x]](../../../_images/math/f9288ec3ac2f52e725d7983a028a993417510e7d.png) , sarà
, sarà 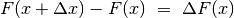 e la densità media sarà:
e la densità media sarà: 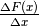 .
.
La densità di probabilità puntuale sarà quindi
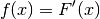
ed ha la caratteristica 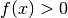 . Per il fatto di determinare, grazie al suo
andamento, la distribuzione dei valori casuali nell’intervallo
. Per il fatto di determinare, grazie al suo
andamento, la distribuzione dei valori casuali nell’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) ,
,
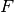 è chiamata funzione di ripartizione.
è chiamata funzione di ripartizione.
Possiamo anche ragionare al contrario, cioè dire che la funzione di ripartizione
relativa al punto ![x\in [a,b]](../../../_images/math/cb9ed72f8db4b1233bb65701d2fc295ba6138b74.png) si ottiene da
si ottiene da
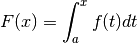
con 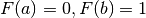 , e quindi
, e quindi
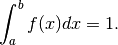
Una funzione 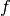 definita su un intervallo
definita su un intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) continua, positiva
e con l’integrale sull’intervallo che vale
continua, positiva
e con l’integrale sull’intervallo che vale 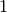 , è una densità di probabilità.
La probabilità che la variabile casuale assuma valori compresi nell’intervallo
, è una densità di probabilità.
La probabilità che la variabile casuale assuma valori compresi nell’intervallo
![[x_1,x_2]](../../../_images/math/841da652fafb7c6737d714236659c5bfc74e87da.png) può essere data in due modi equivalenti: o integrando la densità
di probabilità oppure calcolando la differenza fra i valori della funzione di
ripartizione. Vale, ancora una volta, il teorema fondamentale del calcolo
integrale:
può essere data in due modi equivalenti: o integrando la densità
di probabilità oppure calcolando la differenza fra i valori della funzione di
ripartizione. Vale, ancora una volta, il teorema fondamentale del calcolo
integrale:
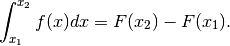
La funzione di ripartizione 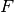 ha per dominio l’intervallo
ha per dominio l’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) e le sue differenze
e le sue differenze 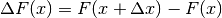 sono proporzionali
al numero di valori che cadono nell’intervallo
sono proporzionali
al numero di valori che cadono nell’intervallo ![[x, x+\Delta x]](../../../_images/math/34cb666357f59d8560db2dbe9249ffa1d65de847.png) , cioè
sono proporzionali a
, cioè
sono proporzionali a 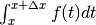 , la probabilità che
la variabile casuale assuma valori in quell’intervallo.
, la probabilità che
la variabile casuale assuma valori in quell’intervallo.
Il procedimento che determina quale sia la funzione di trasformazione 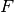 necessaria a determinare una certa distribuzione di valori in
necessaria a determinare una certa distribuzione di valori in ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) è
il seguente:
è
il seguente:
- Si parte da una funzione f che esprime la densità. Essa deve essere:
![f:[a,b]\to \mathbf{R}](../../../_images/math/86bbcc1e6fd1ad5fca5cf93f9037be22a7432370.png) , continua, positiva e con
, continua, positiva e con 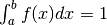 .
Se manca quest’ultima condizione, per esempio in una diversa funzione
.
Se manca quest’ultima condizione, per esempio in una diversa funzione 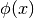 ,
si può operare in modo da ottenere
,
si può operare in modo da ottenere 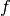 in questo modo:
in questo modo:
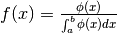 .
. - Si considera la funzione di ripartizione
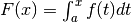 che
risulta automaticamente continua, invertibile e con
che
risulta automaticamente continua, invertibile e con 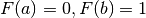 .
. - Si ricava la sua inversa
![F^{-1}:[0,1]\to [a,b]](../../../_images/math/b4faffa343551a9dfa7d495f7b26f70891b15de7.png) e la si applica ai
valori pseudocasuali
e la si applica ai
valori pseudocasuali 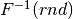 .
.
Esempi¶
Una funzione di prova¶
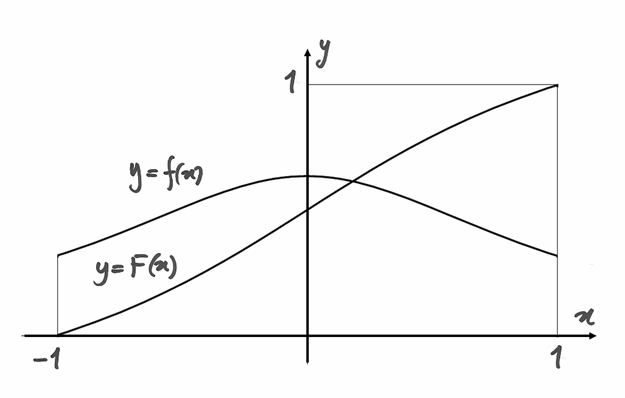
La funzione 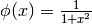 nell’intervallo
nell’intervallo ![[-1,1]](../../../_images/math/11d586f6b5c3a0445fa328423430a9390fd2834b.png) è pari
e ha un massimo assoluto per
è pari
e ha un massimo assoluto per 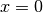 , è continua e positiva ma non è una
densità di probabilità, perché
, è continua e positiva ma non è una
densità di probabilità, perché
![\int_{-1}^1\frac{dx}{1+x^2}=2\int_0^1\frac{dx}{1+x^2}=2[\arctan x]_0^1=\frac{\pi}{2}.](../../../_images/math/8118708b3e97fca4d73bd9e32164fff4d7296819.png)
Allora trasformiamo 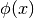 in una funzione di densità:
in una funzione di densità:
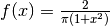 . La funzione di ripartizione è allora:
. La funzione di ripartizione è allora:
![F(x)=\int_{-1}^x\frac{2}{\pi(1+t^2)}dt=\frac{2}{\pi}[\arctan]_{-1}^x=
\frac{2}{\pi}\left(\arctan x +\frac{\pi}{4} \right)=
\frac{2}{\pi}\arctan x+\frac{1}{2}.](../../../_images/math/83e6e511685482ddb3fdbb418650ab0810626c9e.png)
Per avere 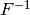 , dobbiamo invertire la funzione
, dobbiamo invertire la funzione 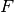
![&y=\frac{2}{\pi}\arctan x+\frac{1}{2}\\
&\frac{2}{\pi}\arctan x=y-\frac{1}{2}\\
&\arctan x=\frac{\pi}{2}\left(y- \frac{1}{2}\right)\\
&x=F^{-1}(y)=\tan\left[\frac{\pi}{2}\left(y-\frac{1}{2} \right) \right].](../../../_images/math/6a3b289cb00956add1df03d29383dcfe71198c94.png)
Poiché la densità di probabilità non ha un picco molto accentuato, la funzione
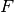 è abbastanza simile a una retta. Cerchiamo allora di accentuare le
differenze e controlliamo i risultati, che otterremo al calcolatore con Derive.
è abbastanza simile a una retta. Cerchiamo allora di accentuare le
differenze e controlliamo i risultati, che otterremo al calcolatore con Derive.
Variando opportunamente...¶
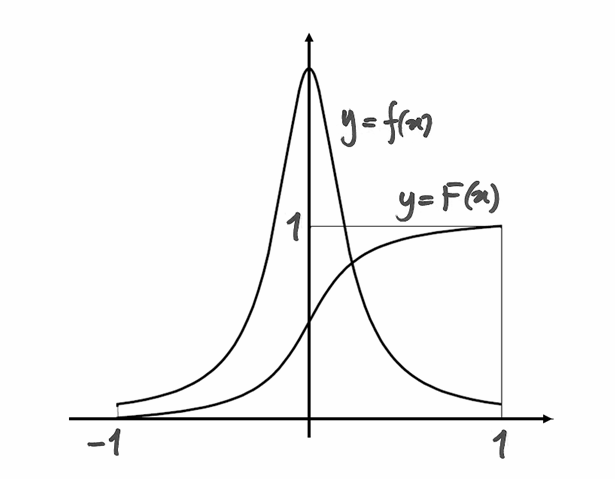
Questa volta 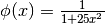 . L’integrale, calcolato con Derive,
risulta
. L’integrale, calcolato con Derive,
risulta 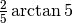 e quindi usiamo, come funzione densità,
e quindi usiamo, come funzione densità,
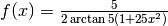 .
.
Da qui, sempre con l’aiuto di Derive, abbiamo:
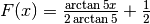 . Seguono i grafici:
. Seguono i grafici:
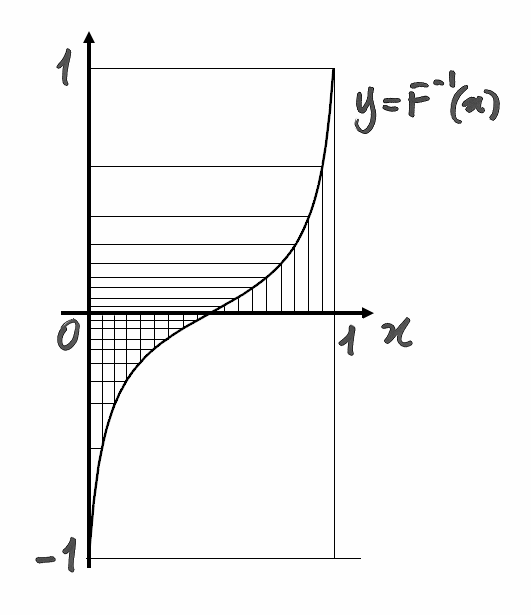
Questa volta il picco di 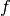 è accentuato, quindi la funzione
è accentuato, quindi la funzione 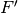 di distribuzione è sufficientemente ondulata. Abbiamo perciò una funzione di
trasferimento
di distribuzione è sufficientemente ondulata. Abbiamo perciò una funzione di
trasferimento 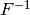 adatta a concentrare i valori (pseudocasuali
trasformati) in una zona ristretta di
adatta a concentrare i valori (pseudocasuali
trasformati) in una zona ristretta di ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , in questo caso la zona
centrale.
, in questo caso la zona
centrale.
![F^{-1}(y)=\frac{1}{5\tan\left[(2y-1)\arctan\frac{1}{5}-\pi y \right]}.](../../../_images/math/309892db767c49b2587e7c07110a463d2c0ea2fe.png)
è la funzione che raccoglie i valori rnd in ![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) e li trasferisce
in
e li trasferisce
in ![[-1,1]](../../../_images/math/11d586f6b5c3a0445fa328423430a9390fd2834b.png) , più densi intorno allo zero e più radi agli estremi.
, più densi intorno allo zero e più radi agli estremi.
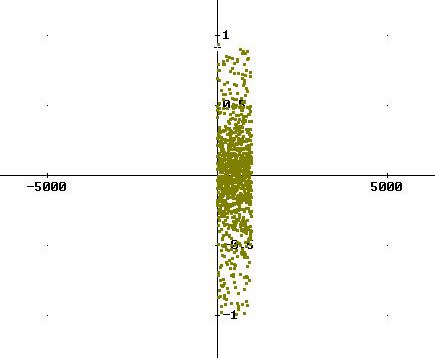
Generaiamo mille valori 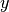 con il solito algoritmo che contiene
con il solito algoritmo che contiene
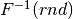 e mettiamo in grafico i punti
e mettiamo in grafico i punti 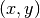 corrispondenti.
Comprimendo il più possibile l’asse orizzontale, si ottiene come risultato della
distribuzione un’immagine piuttosto evidente.
corrispondenti.
Comprimendo il più possibile l’asse orizzontale, si ottiene come risultato della
distribuzione un’immagine piuttosto evidente.
Riassunto¶
- Ci sono metodi approssimati per calcolare un integrale, utili quando non si è in grado di esprimere la primitiva. Si tratta di metodi numerici, cioè di algoritmi realizzati attraverso un linguaggio di programmazione. Sono efficaci, ma la loro efficienza varia a seconda del metodo.
- Il metodo dei rettangoli approssima l’integrale realizzando un ricoprimento
fatto a rettangoli dell’area da calcolare, detta trapezoide. Se i rettangoli
hanno tutti uguale base
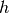 , la formula di riferimento è:
, la formula di riferimento è:
Il metodo dei trapezi realizza un’approssimazione migliore. I rettangoli sono sostituiti da trapezi, quindi il grafico di
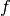 è approssimato da una spezzata,
cioè dal grafico di una funzione a dominio discreto
è approssimato da una spezzata,
cioè dal grafico di una funzione a dominio discreto 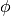 . La formula di
riferimento per realizzare l’algoritmo, nel caso di
. La formula di
riferimento per realizzare l’algoritmo, nel caso di 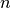 trapezi di altezza
trapezi di altezza
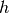 costante, è:
costante, è:![\int_a^bf(x)dx\cong \frac{h}{2}\left[y_0+2\sum_1^{n-1}y_k+y_n \right].](../../../_images/math/1202143eed3e9a601260eb3c2a901374810026ee.png)
L’approssimazione polinomiale è il metodo che permette di sostituire tratti del grafico di
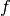 con archi del grafico di polinomi. Nel caso di
archi di parabola, il metodo si dice di integrazione parabolica e la formula di
riferimento si chiama formula di Simpson:
con archi del grafico di polinomi. Nel caso di
archi di parabola, il metodo si dice di integrazione parabolica e la formula di
riferimento si chiama formula di Simpson:![\int_a^bf(x)dx\cong \frac{h}{3}\left[y_0+4\sum_1^m y_{2k-1}+2\sum_1^{m-1}y_{2k}+y_{2m} \right].](../../../_images/math/95953d68063c6f7d9912555a20aa952ccdb96769.png)
L’algoritmo realtivo fornisce l’integrale esatto dei polinomi fino al terzo grado e la sua efficienza è notevolmente superiore agli altri metodi descritti.
Il metodo Montecarlo è un metodo statistico. La superficie di cui si cerca l’area viene pensata come un bersaglio da colpire con lanci casuali. Ogni lancio individua un punto del piano entro la superficie o fuori di essa. Alla termine del gruppo di lanci si fa il conteggio di quanti sono andati a bersaglio, sul totale. Il risultato è proporzionale al valore dell’integrale. L’essenza del metodo è la generazione di numeri casuali, che avviene attraverso il software: la funzione che li esprimne è random (rnd). La formula di riferimento è:
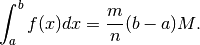
Il metodo Montecarlo non è di grande precisione, ma è semplice ed efficiente. Viene usato per avere una rapida stima di integrali difficili.
Esistono software specializzati per la matematica che risolvono con grande efficienza anche integrali definiti e indefiniti. La loro efficienza è di molti ordini di grandezza superiore a quelli realizzzati dai nostri algoritmi. Uno di questi è Derive.
La generazione di numeri casuali viene simulata dai software: per questo si chiamano più correttamente pseudocasuali. Sono numeri nell’intervallo
![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) , le cui
sequenze iniziano a ripetersi dopo milioni di numeri. La simulazione della casualità
è affidabile, perchè ogni numero è indipendente dai precedenti e le sequenze generate
sono omogenee, cioè ricoprono l’intervallo con uguale densità.
, le cui
sequenze iniziano a ripetersi dopo milioni di numeri. La simulazione della casualità
è affidabile, perchè ogni numero è indipendente dai precedenti e le sequenze generate
sono omogenee, cioè ricoprono l’intervallo con uguale densità.L’intervallo di integrazione
![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) è in genere diverso dall’intervallo
è in genere diverso dall’intervallo ![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) dei numeri rnd. La funzione che trasforma un rnd in modo che appartenga ad
dei numeri rnd. La funzione che trasforma un rnd in modo che appartenga ad ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) è
è 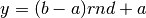 .
.Si può modificare questa funzione, quando si vuole una particolare densità in
![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , in modo che sia disomogeneo secondo una certa legge.
Il procedimento è spiegato in dettaglio nel Par.10.6.
, in modo che sia disomogeneo secondo una certa legge.
Il procedimento è spiegato in dettaglio nel Par.10.6.
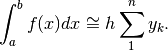
.png)